Статические (нижний
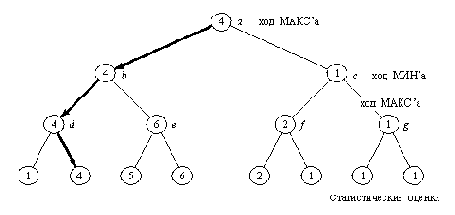
Рисунок 15. 2. Статические (нижний уровень) и минимаксные рабочие
оценки вершин дерева поиска. Выделенные ходы образуют основной
вариант, т. е. минимаксно-оптимальную игру с обеих сторон.
Мы различаем два вида оценок: оценки вершин нижнего уровня и оценки внутренних вершин (рабочие оценки). Первые из них называются также "статическими", так как они вычисляются при помощи "статической" оценочной функции, в противоположность рабочим оценкам, получаемым "динамически" при распространении статических оценок вверх по дереву.
Правила распространения оценок можно сформулировать следующим образом. Будем обозначать статическую оценку позиции Р через v( P), а ее рабочую оценку - через V( Р). Пусть Р1, ..., Рn - разрешенные преемники позиции Р. Тогда соотношения между статическими и рабочими оценками можно записать так:
V( Р) = v( P)
если Р - терминальная позиция дерева поиска (n=0)
V( Р) = max V( Рi
)
i
если P - позиция с ходом МАКС'а
V( Р) = min V( Рi
)
i
если Р - позиция с ходом МИН'а
line();% Минимаксная процедура: минимакс( Поз, ЛучшПоз, Оц)
% Поз - позиция, Оц - ее минимаксная оценка;
% лучший ход из Поз ведет в позицию ЛучшПоз
минимакс( Поз, ЛучшПоз, Оц) :-
ходы( Поз, СписПоз), !,
% СписПоз - список разрешенных ходов
лучш( СписПоз, ЛучшПоз, Оц);
стат_оц( Поз, Оц).
% Поз не имеет преемников
лучш( [Поз], Поз, Оц) :-
минимакс( Поз, _, Оц), !.
лучш( [Поз1 | СписПоз], ЛучшПоз, ЛучшОц) :-
минимакс( Поз1, _, Оц1),
лучш( СписПоз, Поз2, Оц2),
выбор( Поз1, Оц1, Поз2, Оц2, ЛучшПоз, ЛучшОц).
выбор( Поз0, Оц0, Поз1, Оц1, Поз0, Оц0) :-
ход_мина( Поз0), Оц > Оц1, !;
ход_макса( Поз0), Оц < Оц1, !.
выбор( Поз0, Оц0, Поз1, Оц1, Поз1, Оц1).
line();
