а) Пример И / ИЛИграфа
Рисунок 13. 4. (а) Пример И / ИЛИ-графа: d, g и h - целевые вершины;
a - исходная задача. (b) и (с) Два решающих дерева, стоимости
которых равны 9 и 8 соответственно. Здесь стоимость решающего
дерева определена как сумма стоимостей всех входящих в него дуг.
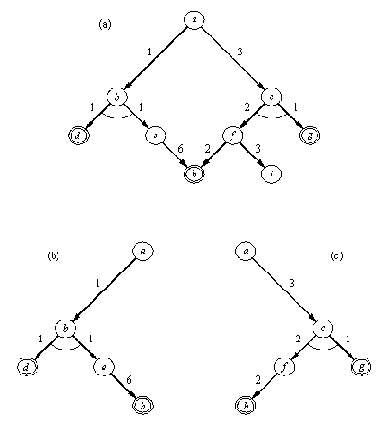
Иллюстрацией к этому определению может служить Рисунок 13.4. Используя стоимости, мы можем формулировать критерии оптимальности решения. Например, можно определить стоимость решающего графа как сумму стоимостей всех входящих в него дуг. Тогда, поскольку обычно мы заинтересованы в минимизации стоимости, мы отдадим предпочтение решающему графу, изображенному на Рисунок 13.4(с).
Однако мы не обязательно должны измерять степень оптимальности решения, базируясь на стоимостях дуг. Иногда более естественным окажется приписывать стоимость не дугам, а вершинам, или же и тем, и другим одновременно.
Подведем итоги:
- И / ИЛИ-представление основано на философии сведения задач к подзадачам.
- Вершины И / ИЛИ-графа соответствуют задачам; связи между вершинами - отношениям между задачами.
- Вершина, из которой выходят ИЛИ-связи, называется ИЛИ-вершиной. Для того, чтобы решить соответствующую задачу, нужно решить одну из ее задач-преемников.
- Вершина, из которой выходят И-связи, называ ется И-вершиной. Для того, чтобы решить соответствующую задачу, нужно решить все ее задачи-преемники.
- При заданном И / ИЛИ-графе конкретная задача специфицируется заданием
стартовой вершины и
целевого условия для распознавания
целевых вершин.
- Целевые вершины (или "терминальные вершины") соответствуют тривиальным (или "примитивным") задачам.
- Решение представляется в виде решающего графа - подграфа всего И / ИЛИ-графа.
- Представление задач в форме пространства состояний можно рассматривать как специальный частный случай И / ИЛИ-представления, когда все вершины И / ИЛИ-графа являются ИЛИ-вершинами.
- И / ИЛИ-представление имеет преимущество в том случае, когда вершинами, находящимися в отношении И, представлены подзадачи, которые можно решать независимо друг от друга. Критерий независимости можно несколько ослабить, а именно потребовать, чтобы существовал такой порядок решения И-задач, при котором решение более "ранних" подзадач не разрушалось бы при решении более "поздних" под задач.
- Дугам или вершинам, или и тем, и другим можно приписать стоимости с целью получить возможность сформулировать критерий оптимальности решения.
