Двоичное дерево
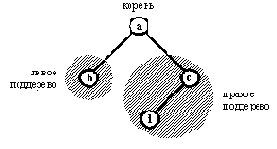
Рисунок 9. 4. Двоичное дерево.
Существует более эффективный и более привычный способ представления двоичных деревьев: нам нужен специальный символ для обозначения пустого дерева и функтор для построения непустого дерева из трех компонент ( корня и двух поддеревьев). Относительно функтора и специального символа сделаем следующий выбор:
- Пусть атом nil представляет пустое дерево.
- В качестве функтора примем дер, так что дерево с корнем X, левым поддеревом L и правым поддеревом R будет иметь вид терма дер( L, X, R) (см. Рисунок 9.5).
В этом представлении дерево Рисунок 9.4 выглядит как
дер( дер( nil, b, nil), a,
дер( дер( nil, d, nil), с, nil) ).
Теперь рассмотрим отношение принадлежности, которое будем обозначать внутри. Цель
внутри( X, Т)
истинна, если Х есть вершина дерева Т. Отношение внутри можно определить при помощи следующих правил:
line();Х есть вершина дерева Т, если
- корень дерева Т совпадает с X, или
- Х - это вершина из левого поддерева, или
- Х - это вершина из правого поддерева.
