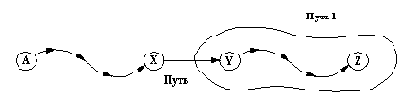
Поиск в графе Граф ациклического пути Путь из А в Z
Рисунок 9. 20. Поиск в графе Граф ациклического пути Путь из А в Z.
На Рисунок 9.20 программа показана полностью. Здесь принадлежит - отношение принадлежности элемента списку. Отношение
смеж( X, Y, G)
означает, что в графе G существует дуга, ведущая из Х в Y. Определение этого отношения зависит от способа представления графа. Если G представлен как пара множеств (вершин и ребер)
G = граф( Верш, Реб)
то
смеж( X, Y, граф( Верш, Реб) ) :-
принадлежит( р( X, Y), Реб);
принадлежит( р( Y, X), Реб).
Классическая задача на графах - поиск Гамильтонова цикла, т.е. ациклического пути, проходящего через все вершины графа. Используя отношение путь, эту задачу можно решить так:
гамильтон( Граф, Путь) :-
путь( _, _, Граф, Путь),
всевершины( Путь, Граф).
всевершины( Путь, Граф) :-
not (вершина( В, Граф),
not принадлежит( В, Путь) ).
Здесь вершина( В, Граф) означает: В - вершина графа Граф.
Каждому пути можно приписать его стоимость. Стоимость пути равна сумме стоимостей входящих в него дуг. Если дугам не приписаны стоимости, то тогда, вместо стоимости, говорят о длине пути.
Для того, чтобы наши отношения путь и путь1 могли работать со стоимостями, их нужно модифицировать, введя дополнительный аргумент для каждого пути:
путь( А, Z, G, Р, С)
путь1( A, P1, C1, G, Р, С)
Здесь С - стоимость пути Р, a C1 - стоимость пути Р1. В отношении смеж также появится дополнительный аргумент, стоимость дуги. На Рисунок 9.21 показана программа поиска пути, которая строит путь и вычисляет его стоимость.
line(); путь( А, Z, Граф, Путь, Ст) :-
путь1( A, [Z], 0, Граф, Путь, Ст).
путь1( А, [А | Путь1], Ст1, Граф, [А | Путь1], Ст).
путь1( А, [Y | Путь1], Ст1, Граф, Путь, Ст) :-
смеж( X, Y, СтXY, Граф),
not принадлежит( X, Путь1),
Ст2 is Ст1 + СтXY,
путь1( А, [ X, Y | Путь1], Ст2, Граф, Путь, Ст).
