а) Граф (b) Направленный граф Каждой дуге приписана ее стоимость
Рисунок 9. 18. (а) Граф. (b) Направленный граф. Каждой дуге приписана ее стоимость.
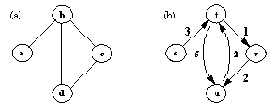
Для представления направленного графа (Рисунок 9.18), применив функторы диграф и д (для дуг), получим
G2 = диграф( [s, t, u, v],
[д( s, t, 3), д( t, v, 1), д( t, u, 5), д( u, t, 2),
д( v, u, 2) ] )
Если каждая вершина графа соединена ребром еще по крайней мере с одной вершиной, то в представлении графа можно опустить множество вершин, поскольку оно неявным образом содержится в списке ребер.
Еще один способ представления графа - связать с каждой вершиной список смежных с ней вершин. В этом случае граф превращается в список пар, каждая из которых состоит из вершины- плюс ее список смежности. Наши графы (Рисунок 9.18), например, можно представить как
G1 = [ a->[b1, b->[a, c, d], c->[b, d], d->[b, c] ]
G2 = [s->[t/3], t->[u/5, v/l], u->[t/2], v->[u/2]]
Здесь символы '->' и '/' - инфиксные операторы.
Какой из способов представления окажется более удобным, зависит от конкретного приложения, а также от того, какие операции имеется в виду выполнять над графами. Вот типичные операции:
- найти путь между двумя заданными вершинами;
- найти подграф, обладающий некоторыми заданными свойствами.
Примером последней операции может служить построение основного дерева графа. В последующих разделах, мы рассмотрим некоторые простые программы для поиска пути в графе и построения основного дерева.
