Внесение Х в двоичный справочник в качестве корня
Рисунок 9. 14. Внесение Х в двоичный справочник в качестве корня.
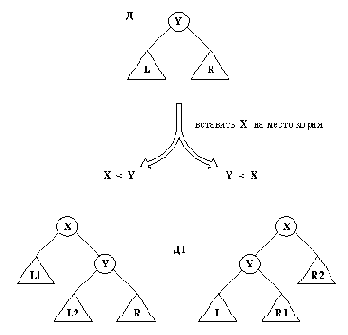
Ответ мы получим, если учтем следующие ограничения на L1, L2:
- L1 и L2 - двоичные справочники;
- множество всех вершин, содержащихся как в L1, так и в L2, совпадает с множеством вершин справочника L;
- все вершины из L1 меньше, чем X; все вершены из L2 больше, чем X.
Отношение, которое способно наложить все эти ограничения на L1, L2, - это как раз и есть наше отношение добкор. Действительно, если бы мы вводили Х в L на место корня, то поддеревьями результирующего дерева как раз и оказались бы L1 и L2. В терминах Пролога L1 и L2 должны быть такими, чтобы достигалась цель
добкор( L, X, дер( L1, X, L2) ).
Те же самые ограничения применимы к R1, R2:
добкор( R, X, дер( R1, X, R2) ).
line(); добавить( Д, X, Д1) :-
% Добавить Х на место корня
добкор( Д, X, Д1).
добавить( дер( L, Y, R), X, дер( L1, Y, R) ) :-
больше( Y, X),
% Ввести Х в левое поддерево
добавить( L, X, L1).
добавить( дер( L, Y, R), X, дер( L, Y, R1) ) :-
больше( X, Y),
% Ввести Х в правое поддерево
добавить( R, X, R1).
добкор( nil, X, дер( nil, X, nil) ). % Ввести Х в пустое дерево
добкор( дер( L, Y, R), Х, дер( L1, Х, дер( L2, Y, R) )) :-
больше( Y, X),
добкор( L, X, дер( L1, X, L2) ).
добкор( дep( L, Y, R), X, дep( дep( L, Y, R1), X, R2) ) :-
больше( X, Y),
добкор( R, X, дер( R1, X, R2) ).
