Сортировка списка процедурой быстрсорт
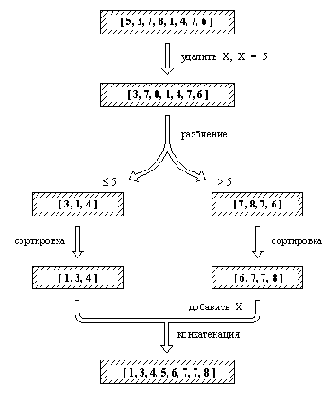
Рисунок 9. 1. Сортировка списка процедурой быстрсорт.
встав( X, [Y | УпорСпис], [Y | УпорСпис1]):-
больше( X, Y), !,
встав( X, УпорСпис, УпорСпис1).
встав( X, УпорСпис, [X | УпорСпис] ).
Процедуры сортировки пузырек и вставсорт просты, но не эффективны. Из этих двух процедур процедура со вставками более эффективна, однако среднее время, необходимое для сортировки списка длиной n процедурой вставсорт, возрастает с ростом n пропорционально n2. Поэтому для длинных списков значительно лучше работает алгоритм быстрой сортировки, основанный на следующей идее (Рисунок 9.1):
line();Для того, чтобы упорядочить непустой список L, необходимо:
(1) Удалить из списка L какой-нибудь элемент Х и разбить оставшуюся часть на два списка, называемые Меньш и Больш, следующим образом: все элементы большие, чем X, принадлежат списку Больш, остальные - списку Меньш.
(2) Отсортировать список Меньш, результат - список УпорМеньш.
(3) Отсортировать список Больш, результат - список УпорБольш.
(4) Получить результирующий упорядоченный список как конкатенацию списков УпорМеньш и [ Х | УпорБольш].
line();Заметим, что если исходный список пуст, то результатом сортировки также будет пустой список. Реализация быстрой сортировки на Прологе показана на Рисунок 9.2. Здесь в качестве элемента X, удаляемого из списка, всегда выбирается просто голова этого списка. Разбиение на два списка запрограммировано как отношение с четырьмя аргументами:
разбиение( X, L, Больш, Меньш).
Временная сложность нашего алгоритма зависит от того, насколько нам повезет при разбиении сортируемого списка. Если списки всегда разбиваются на два списка примерно равной длины, то процедура сортировки имеет временную сложность порядка nlogn, где n - длина исходного списка. Если же, наоборот, разбиение всегда приводит к тому, что один из списков оказывается значительно больше другого, то сложность будет порядка n2. Анализ показывает, что, к счастью, средняя производительность быстрой сортировки ближе к лучшему случаю, чем к худшему.
Программу, показанную на Рисунок 9.2, можно усовершенствовать, если реализовать операцию конкатенации более эффективно. Напомним, что конкатенация
line();быстрсорт( [ ], [ ] ).
быстрсорт( [X | Хвост], УпорСпис) :-
разбиение( X, Хвост, Меньш, Больш),
быстрсорт( Меньш, УпорМеньш),
быстрсорт( Больш, УпорБольш),
конк( УпорМеньш, [X | УпорБольш], УпорСпис).
разбиение( X, [ ], [ ], [ ] ).
разбиение( X, [Y | Хвост], [Y | Меньш], Больш ) :-
больше( X, Y), !,
разбиение( X, Хвост, Меньш, Больш).
разбиение( X, [Y | Хвост], Меньш, [Y | Больш] ) :-
разбиение( X, Хвост, Меньш, Больш).
конк( [ ], L, L).
конк( [X | L1], L2, [X | L3] ) :-
конк( L1, L2, L3 ).
