Двухступенчатая функция
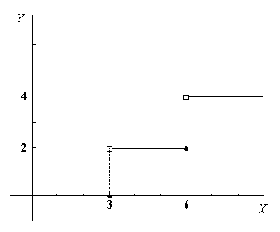
Рисунок 5. 1. Двухступенчатая функция
неэффективности программы. Поэтому иногда требуется его ограничить или исключить вовсе. Для этого в Прологе предусмотрена конструкция "отсечение".
Давайте сначала рассмотрим простую программу, процесс вычислений, по которой содержит ненужный перебор. Мы выделим те точки этого процесса, где перебор бесполезен и ведет к неэффективности.
Рассмотрим двухступенчатую функцию, изображенную на Рисунок 5.1. Связь между Х и Y можно определить с помощью следующих трех правил:
Правило 1: если Х < 3, то Y = 0
Правило 2: если 3 <= X и Х < 6, то Y = 2
Правило 3: если 6 <= X, то Y = 4
На Прологе это можно выразите с помощью бинарного отношения
f( X, Y)
так:
f( X, 0) :- X < 3. % Правило 1
f( X, 2) :- 3 =< X, X < 6. % Правило 2
f( X, 4) :- 6 =< X. % Правило 3
В этой программе предполагается, конечно, что к моменту начала вычисления f( X, Y) Х уже конкретизирован каким-либо числом; это необходимо для выполнения операторов сравнения.
Мы проделаем с этой программой два эксперимента. Каждый из них обнаружит в ней свой источник неэффективности, и мы устраним оба этих источника по очереди, применив оператор отсечения.
