Решение задачи о восьми
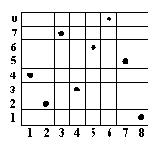
Рисунок 4. 6. Решение задачи о восьми ферзях. Эта позиция может быть
представлена в виде списка [1/4, 2/2, 3/7, 4/3, 5/6, 6/8, 7/5, 8/1].
Нас интересует решение для доске размером 8х8. Однако, как это часто бывает в программировании, ключ к решению легче найти, рассмотрев более общую постановку задачи. Как это ни парадоксально, но часто оказывается, что решение более общей задачи легче сформулировать, чем решение более частной, исходной задачи; после этого исходная задача решается просто как частный случай общей задачи.
Основная часть работы при таком подходе ложится на нахождение правильного обобщения исходной задачи. В нашем случае хорошей является идея обобщать задачу в отношении количества ферзей (количества вертикалей в списке), разрешив количеству ферзей принимать любое значение, включая нуль. Тогда отношение решение можно сформулировать, рассмотрев два случая:
Случай 1. Список ферзей пуст. Пустой список без сомнения является решением, поскольку нападений в этом случае нет.
Случай 2. Список ферзей не пуст. Тогда он выглядит так:
[ X/Y | Остальные ]
В случае 2 первый ферзь находится на поле Х / Y, а остальные - на полях, указанных в списке Остальные. Если мы хотим, чтобы это было решением, то должны выполняться следующие условия:
(1) Ферзи, перечисленные в списке Остальные, не должны бить друг друга; т. е. список Остальные сам должен быть решением.
(2) Х и Y должны быть целыми числами от 1 до 8.
(3) Ферзь, стоящий на поле X / Y, не должен бить ни одного ферзя из списка Остальные.
Чтобы запрограммировать первое условие, можно воспользоваться самим отношением решение. Второе условие можно сформулировать так: Y должен принадлежать списку целых чисел от 1 до 8. т. е. [1, 2, 3, 4, 5, 6, 7, 8]. С другой стороны, о координате Х можно не беспокоиться, поскольку список-решение должен соответствовать шаблону, у которого Х-координаты уже определены. Поэтому Х гарантированно получит правильное значение от 1 до 8. Третье условие можно обеспечить с помощью нового отношения небьет. Все это можно записать на Прологе так:
решение( [X/Y | Остальные] ) :-
решение( Остальные),
принадлежит( Y, [1, 2, 3, 4, 5, 6, 7, 8] ),
небьет( X/Y, Остальные).
Осталось определить отношение небьет:
небьет( Ф, Фспис)
И снова его описание можно разбить на два случая:
(1) Если список Фспис пуст, то отношение, конечно, выполнено, потому что некого бить (нет ферзя, на которого можно было бы напасть).
(2) Если Фспис не пуст, то он имеет форму
[Ф1 | Фспис1]
и должны выполняться два условия:
(а) ферзь на поле Ф не должен бить ферзя на поле Ф1 и
(b) ферзь на поле Ф не должен бить ни одного ферзя из списка Фспис1.
Выразить требование, чтобы ферзь, находящийся на некотором поле, не бил другое поле, довольно просто: эти поля не должны находиться на одной и той же горизонтали, вертикали или диагонали: Наш шаблон решения гарантирует, что все ферзи находятся на разных вертикалях, поэтому остается только обеспечить, чтобы
- Y-координаты ферзей были различны и
- ферзи не находились на одной диагонали, т.е. расстояние между полями по направлению Х не должно равняться расстоянию между ними по Y.
На Рисунок 4.7 приведен полный текст программы. Чтобы облегчить ее использование, необходимо добавить список-шаблон. Это можно сделать в запросе на генерацию решений. Итак:
?- шаблон( S), решение( S).
line();решение( [ ] ).
решение( [X/Y | Остальные ] ) :-
% Первый ферзь на поле X/Y,
% остальные ферзи на полях из списка Остальные
решение( Остальные),
принадлежит Y, [1, 2, 3, 4, 5, 6, 7, 8] ),
небьет( X/Y | Остальные).
% Первый ферзь не бьет остальных
небьет( _, [ ]). % Некого бить
небьет( X/Y, [X1/Y1 | Остальные] ) :-
Y =\= Y1,
% Разные Y-координаты
Y1-Y =\= X1-X
% Разные диагонали
Y1-Y =\= X-X1,
небьет( X/Y, Остальные).
принадлежит( X, [X | L] ).
принадлежит( X, [Y | L] ) :-
принадлежит( X, L).
% Шаблон решения
шаблон( [1/Y1, 2/Y2, 3/Y3, 4/Y4, 5/Y5, 6/Y6, 7/Y7, 8/Y8]).
line();
