В поисках аксиом
Для понимания природы математической достоверности очень поучительно довести до конца разбор утверждения E1. Поскольку у нас все-таки остались некоторые сомнения относительно абсолютной необходимости пересечения окружности на рис. 10.3, попробуем представить себе ситуацию, когда они не пересекаются. Полная неудача этой попытки будет означать, что утверждение E1 математически достоверно и не может быть разложено на более простые утверждения; тогда его следует принять в качестве аксиомы. Если же нам ценой большего или меньшего насилия над воображением удастся представить себе ситуацию, в которой ?A и ?B не пересекаются, эта ситуация, надо полагать, придет в противоречие с какими-то более простыми и глубокими утверждениями, обладающими математической достоверностью; тогда мы их и примем за аксиомы, а наличие противоречия будет служить доказательством E1. Таков обычный путь к установлению аксиом в математике.
Проведем сначала окружность ?A. Затем поставим опорную ножку циркуля в точку B, а пишущую — в точку A и начнем проводить окружность ?B. Мы движемся от центра окружности ?A к ее периферии и в некоторый момент (так мы представляем это в своем воображении) должны либо пересечь окружность ?A, либо как-то перескочить через нее, разорвав для этого окружность ?A и ?B (рис. 10.4). Но окружность ?A мы воображаем как непрерывную линию и нам становится ясно, что свойства непрерывности, являющиеся более фундаментальными и общими, чем другие особенности данной задачи, лежат в основе нашей уверенности в пересечении окружностей ?A и ?B. Поэтому поставим перед собой цель доказать утверждение e1 исходя из свойств непрерывности окружности. Нам понадобятся при этом некоторые соображения, связанные с порядком расположения точек на прямой. Понятие непрерывности и порядка мы включаем в число основных неопределяемых понятий геометрии, подобно понятиям точки, прямой, расстояния и т. д.
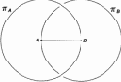
Рис. 10.4. «Перескакивающие» окружности
Вот один из возможных путей к цели.
Введем понятие «внутри» (применительно к окружности) с помощью следующего определения:
O1: Говорят, что точка A лежит внутри окружности ?, если она не лежит на ? и любая прямая, проходящая через точку A, пересекает ? двух точках, причем таким образом, что точка A лежит между точками пересечения. Если точка лежит не на окружности и не внутри нее, то говорят, что она лежит вне окружности. Понятие «между» характеризует порядок расположения трех точек на прямой. Можно принять его за основное, а можно выразить через более общее понятие «порядок» путем следующего определения:
O2: Говорят, что точка A находится между точками B1 и B2, если эти три точки расположены на одной прямой и при движении по ней встречаются в порядке B1, A, B2 или B2, A, B1
Примем в качестве аксиом следующие положения:
A1: Центр окружности лежит внутри нее.
A2: Дуга окружности, соединяющая любые ее точки, непрерывна.
A3: Если точка A лежит внутри окружности ?, а точка B - вне окружности и эти две точки соединяет непрерывная линия, то существует точка пересечения этой линии с окружностью.
Опираясь на эти аксиомы, приступаем к доказательству. Окружность ?B по условию задачи проходит через центр A окружности ?A. Если у нас будет уверенность, что существует хотя бы одна точка окружности ?B, не лежащая внутри ?A, то мы докажем E1. Действительно, если она лежит на ?A, то E1 уже имеет место. Если она лежит вне ?A, то дуга окружности ?B соединяет ее с центром, т. е. с внутренней точкой окружности ?A. Следовательно, по аксиомам A2 и A3 существует точка пересечения ?A и ?B.
Но можем ли мы быть уверены, что существует точка на окружности ?B, находящаяся вне ?A? Попытаемся вообразить противоположный случай. Он представлен на рис. 10.5. Это вторая попытка вообразить ситуацию, противоречащую доказываемому утверждению. Если первая попытка немедленно вступила в явное противоречие с непрерывностью окружности, то вторая оказалась более успешной. В самом деле, мы с некоторой натяжкой можем представить, что так получится. Берем циркуль, острие его ставим в точку B, карандаш — в точку A.
Начинаем проводить окружность, не отрывая карандаша от бумаги, а когда карандаш возвращается на уже начерченную линию, снимаем
циркуль и видим, что получился рис. 10.5. А почему бы и нет?
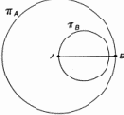
Рис. 10.5. Окружность ?B внутри ?A
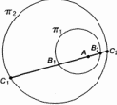
Рис. 10.6. К доказательству теоремы T1
Чтобы доказать, что это невозможно, надо доказать, что в этом случае центр окружности ?B обязательно окажется вне ее. Нам поможет в этом следующая теорема:
T1: Если окружность ?1 лежит целиком внутри окружности ?2, то каждая внутренняя точка окружности ?1 является также внутренней точкой окружности ?2.
Для ее доказательства выберем произвольную внутреннюю точку A окружности ?1 (рис. 10.6). Проведем через нее прямую. По определению O1 она пересечет ?1 в двух точках: B1 и B2. Так как B1 (как и B2) лежит внутри ?2, эта прямая пересечет также ?2 в двух точках: C1 и C2. Мы получили пять точек на прямой, связанных следующими отношениями порядка: A лежит между B1 и B2; B1 и B2 лежат между C1 и C2. Тот факт, что в этой ситуации точка A оказывается между точками C1 и C2 представляется нам столь очевидным и первичным, что мы смело формулируем его как еще одну аксиому.
A4: Если на одной прямой обе точки B1 и B2 лежат между точками C1 и C2, то и любая точка A, лежащая между B1 и B2, лежит также между C1 и C2.
Поскольку в качестве A мы можем взять любую точку внутри ?1 и провести через нее любую прямую, теорема T1 доказана.
Теперь легко закончить доказательство E1. Если окружность ?B лежит целиком внутри ?A, то по теореме T1 и центр ее B должен лежать внутри ?B. Однако по условию задачи точка B находится на ?A. Следовательно, ?B содержит хотя бы одну точку, не являющуюся внутренней к ?A.
Итак, чтобы доказать одно утверждение E1 нам понадобилось целых четыре утверждения A1 — A4, но зато эти утверждения выражают чрезвычайно глубокие и общие модели действительности, связанные с понятиями непрерывности и порядка. Мы не можем даже представить себе, чтобы они были ложными. Некоторые претензии можно предъявить разве только к аксиоме A1, которая связывает понятие центра, имеющее метрическую природу (т.
е. включающее понятие измерения), с понятием «внутри», опирающимся исключительно на понятия непрерывности и порядка. Можно пожелать, чтобы эта связь была осуществлена с помощью более простых геометрических объектов в более легких условиях для работы воображения. Пожелание это легко выполнимо. Заменим аксиому A1 следующей аксиомой
A'1 : Если на прямой дана точка A и некоторое расстояние (отрезок) Р, то существует ровно две точки на прямой, расположенные на расстоянии Р от точки A, причем точка A лежит между этими двумя точками.
Опираясь на эту аксиому, докажем утверждение A1 как теорему. Проведем через центр окружности произвольную прямую. По аксиоме A'1, на ней будут две точки, расположенные на расстоянии R (радиус окружности) от центра. Так как окружность определяется как множество точек, находящихся на расстоянии R от центра, эти точки принадлежат окружности. По аксиоме A'1 точка центра лежит между ними и, следовательно, по определению O1 является внутренней точкой. Таким образом, аксиома A1 сведена к аксиоме A'1. Попробуйте теперь вообразить точку на прямой, которая не имеет двух точек, расположенных от нее по разные стороны на заданном расстоянии!
