Декарт и Ферма
Очень поучительно сравнить математические работы Декарта и Ферма. Как математик Ферма был не менее, а, пожалуй, более одаренным, чем Декарт. Это видно из его замечательных работ по теории чисел. Но он был восхищенным поклонником греков и продолжателем их традиций. Свои открытия по теории чисел Ферма изложил в замечаниях на полях «Арифметики» Диофанта. Его работы по геометрии возникли в результате усилий доказать некоторые положения, на которые Папп ссылался как на принадлежащие Аполлонию, не приводя, однако, доказательства. Размышляя над этими проблемами, Ферма стал систематически использовать представление положения точки на плоскости длинами двух отрезков — абсциссы и ординаты и представление кривой в виде уравнения, связывающего эти отрезки. Идея эта с геометрической точки зрения отнюдь не была новой: она является стержневой не только у Аполлония, но уже у Архимеда и восходит к еще более древним авторам. Архимед описывает конические сечения через их «симптомы», т. е. пропорции, связывающие абсциссы и ординаты точек. Возьмем, например, эллипс с большой осью AB (рис. 11.3). Перпендикуляр PQ, опущенный из некоторой точки эллипса Р на ось AB, называется «ординатой», а отрезки AQ и QB — «абсциссами» этой точки (оба термина — латинские переводы греческих терминов Архимеда). Отношение площади квадрата, построенного на ординате, к площади прямоугольника, построенного на двух абсциссах, одинаково для всех точек Р, лежащих на эллипсе. Это и есть «симптом» эллипса, т. е. по существу уравнение. Его можно записать в виде
y2 : (x1 × x2) = const.
Аналогичные симптомы устанавливаются для гиперболы и параболы. Чем это не система координат?
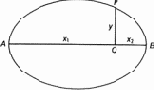
Рис. 11.3. Ордината и абсциссы эллипса
Ферма в отличие от древних формулирует симптомы не в виде словесно описанных пропорций, а в виде уравнений на языке Виета. Это облегчает преобразования; в частности, сразу видно, что вместо двух абсцисс удобнее оставить одну. Но подход остается чисто геометрическим, пространственным.
Ферма изложил свои идеи в трактате «Введение в изучение плоских и телесных мест».
Он был опубликован только в 1679 г. уже после смерти автора, но стал известен французским математикам еще в 30-х годах, несколько раньше, чем математические работы Декарта.
Знаменитая «Геометрия» Декарта вышла в свет в 1637 г. Никакого влияния со стороны Ферма Декарт, конечно, не испытал (неизвестно даже, читал ли он трактат Ферма); метод Декарта сложился задолго до выхода «Геометрии», еще в 20-х годах. Тем не менее, собственно геометрические идеи Декарта и Ферма практически тождественны. Но Декарт создал новую алгебру, основанную на понятии отношения геометрических величин. У Виета можно складывать и вычитать только однородные величины и в коэффициенты обязательно включается указание на их геометрическую природу. Например, уравнение, которое мы записали бы в виде
A3 + BA = D,
Виет записывал так:
A cubus +B planum in A aequatur D solido,
т. е. к кубу с ребром A прибавить площадь B, помноженную на A, равно объему D. Виет и Ферма идейно находятся в плену геометрической алгебры греков. Декарт решительно порывает с ней. Отношения, с которыми имеет дело алгебра Декарта, не геометрические пространственные объекты, а умозрительные понятия — «числа». Он не стеснен требованием однородности слагаемых и вообще требованием пространственной интерпретации; возведение в степень он понимает как многократное умножение и указывает число множителей маленькой цифрой выше и правее переменной. Символика Декарта практически совпадает с современной.
